论文提出了一种针对两轮多重签名(Multi-signature)的亚指数时间攻击算法，攻击者可以通过并发来伪造任意消息上的多重签名。这种攻击方法能够广泛应用在当时已有的两轮多重签名方案中，其中包括了许多有名方案，如CoSi, BCJ, MuSig-1等，安全性受到影响的还有其它使用了这些多重签名的协议，如RandHound.

Title: On the Security of Two-Round Multi-Signatures

Author: Manu Drijvers, Kasra Edalatnejad and Bryan Ford etc.

Publication: S&P 2019

Link: https://eprint.iacr.org/2018/417.pdf

CoSi多重签名

CoSi在2016年由Syta等人提出，它仅仅是把Schnorr签名中的每一个量拆分成签名方的份额，最后由一个签名参与方统一地聚合起来发布，所以是一种plain的Schnorr多重签名方案.

参数生成 ：选择$q$阶群$\mathbb{G}$，$q$为素数，$g$是$\mathbb{G}$的一个随机生成元。选择两个哈希函数$H_0,H_1:\{0,1\}^\ast \rightarrow \mathbb{Z}_q$。输出公共参数$par\leftarrow (\mathbb{G},g,q,H_0,H_1)$.

密钥生成 ：CoSi的每一方都要执行密钥生成算法。参与方$P_i$随机选择私钥$sk_i\leftarrow \mathbb{Z}_q$并且计算公钥$y_i\leftarrow g^{sk_{i}}$。此外还需附上对$sk_i$知识的证明：随机选择$r_i\leftarrow \mathbb{Z}_q$，计算$c_i\leftarrow H_0(g^r,y_i)$以及$s_i\leftarrow r_i+c_i \cdot sk_i$，将$(c_i,s_i)$作为证明$\pi_i$。最终输出$pk_i\leftarrow(y_i,\pi_i)$和$sk_i$作为公私钥对。

(注：这里对私钥知识的证明是为了防止敌手看见其它参与方生成的公钥后，自适应地选择自己的公钥，即防止rogue-key攻击)

分布式签名

为了减少各方之间的通信量，CoSi采用了树形的结构，消息由根节点向叶子结点传播，由父节点传播给它所有的子节点，或者叶子节点向根节点传播，由每一个子节点传播给它的父节点。总共分为4阶段，如下面的图所示(父节点负责聚合子节点消息，再传播给上一层，图中没有展示这一过程).

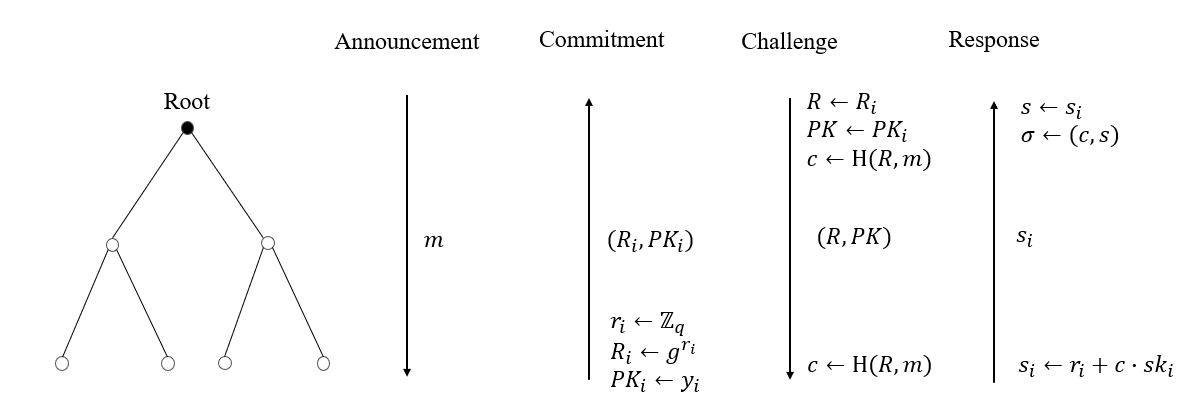
• Announment：由根节点向叶子节点传播。从根节点出发，由上往下发送待签名的消息$m$以及唯一的会话标识符$sid$.
• Commitment：由叶子节点向根节点传播。从叶子节点出发，每个子节点随机选择$r_i\leftarrow \mathbb{Z}_q$，计算Schnorr签名中的nonce份额$R_i\leftarrow g^{r_i}$，从$pk_i$提取出$y_i$的部分，作为签名的公钥份额$PK_i$。子节点将$(R_i,PK_i)$发送给它的父节点.
• Challenge：由根节点向叶子节点传播。根节点作为最后完成聚合的一方，它用自己的nonce份额$R_i^{\prime}$和收到的$R_i$计算全局的$R$，同样得到全局的公钥$PK$，挑战$c\leftarrow H_0(R,m)$。从根节点出发，每个父节点将$(R,PK)$发送给它所有的子节点，子节点收到后，计算挑战$c$.
• Response：由叶子节点向根节点传播。Challenge阶段结束后，从叶子节点出发，每个子节点计算各自的签名份额$s_i\leftarrow r_i+c\cdot sk_i$。最终由根节点聚合所有的$s_i$得到最终的$s$，发布签名$\sigma=(c,s)$.

签名验证

CoSi的验证和Schnorr的验证一样，对消息$m$和签名$\sigma=(c,s)$：

$$c \overset{?}{=} H_0(g^s\cdot PK^{-c},m)$$

针对CoSi的攻击

从表面上看，CoSi只是简单地以分布式的方式完成了Schnorr签名，Schnorr签名安全似乎CoSi也安全。然而正如这篇论文所说，CoSi安全性存在问题，事实上CoSi的原论文中并没有给出正式的归约证明.

考虑树只有根节点的参与方是恶意的，其余节点是诚实方的情况。由于CoSi从下往上聚合，所以现在可以假设只有两个参与方：一个是伪造签名的敌手$\mathcal{A}$，位于根节点；另一个是诚实的挑战方，位于叶子结点.

攻击的大体思路是由$\mathcal{A}$开启$k-1$次并行执行，与挑战方交互在相同$m$上生成$k-1$个签名(可以看作是将$sk^\ast $嵌入到了签名Oracle中，$\mathcal{A}$访问$k-1$次签名Oracle)，利用这些信息伪造消息$m^\ast \not = m$上的签名。第$i$次执行过程如下图所示，$i\in\{1,2,…,k-1\}$。其中$P_1$是敌手$\mathcal{A}$，所拥有密钥$sk_1$，$P_2$是挑战者，虚线框内为协议正常执行的步骤，所拥有密钥$sk^\ast $.

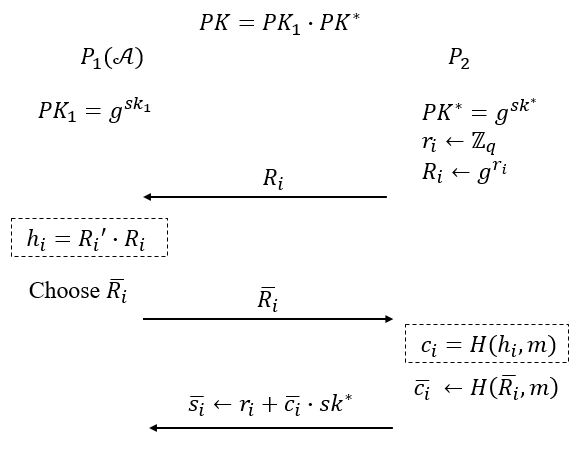
因为$\mathcal{A}$位于根节点，最终的$R$由根节点发布，所以其它节点的承诺份额对它来说没有任何意义。所以$\mathcal{A}$每次执行选择设计好的$\bar{R}$，来达到攻击的目的，思路类似于对公钥的rogue-key攻击.

在Response阶段，$\mathcal{A}$获得来自挑战者$k-1$次执行的$\bar{s_i}=r_i+\bar{c_i}\cdot sk^\ast $。观察$r_i$是挑战者选择的，对$\mathcal{A}$不可见，$\bar{c_i}$是在$\mathcal{A}$的错误的$\bar{R_i}$上生成的散列值，并且满足$\bar{c_i}=H(\bar{R_i},m)$.

回顾Schnorr签名$\sigma=(c,s)$的验证：

$$\begin{aligned} R&=g^s\cdot PK^{-c} \\ c^{\prime}&=H(R,m) \\ c&\overset{?}{=}c^{\prime} \end{aligned}$$

那么对每一轮来说，仍然有：

$$\begin{aligned} \bar{R_i}&=g^{\bar{s_i}}\cdot ({PK^{*}})^{-\bar{c_i}} \\ \bar{c_i} &=H(\bar{R_i},m) \end{aligned}$$

成立。只是不再满足$\bar{c_i}\not =H(R_i,m)$。$\mathcal{A}$将这$k-1$轮结果聚合起来：

$$\begin{aligned} \prod_{i=1}^{k-1}R_i&=g^{\sum_{i=1}^{k-1}\bar{s_i}}\cdot ({PK^{*}})^{-\sum_{i=1}^{k-1}\bar{c_i}} \\ \end{aligned}$$

现在考虑如果$\mathcal{A}$要成功伪造在$m^\ast $上的签名$\sigma^\ast =(c^\ast ,s^\ast )$，如果诚实生成的$\prod_{i=1}^{k-1}R_i$作为伪造时的$R^\ast $，$PK$是全局的公钥$g^{sk^\ast +sk_1}$，那么$c^\ast $和$s^\ast $应该满足的验证条件：

$$\begin{aligned} \prod_{i=1}^{k-1}R_i&=g^{s^{*}}\cdot (PK)^{-c^{*}} \\ c^{*}&=H(\prod_{i=1}^{k-1}R_i,m^{*}) \end{aligned}$$

如果令$c^\ast =\sum_{i=1}^{k-1}\bar{c_i}$，那么$s^\ast $：

$$\begin{aligned} s^{*}&= \sum_{i=1}^{k-1}r_i +{\sum_{i=1}^{k-1}\bar{c_i}}\cdot (sk^{*}+sk_1)\\ &=\sum_{i=1}^{k-1}r_i+\sum_{i=1}^{k-1}\bar{c_i}\cdot sk^{*}+c^{*}\cdot sk_1 \\ &=\sum_{i=1}^{k-1}\bar{s_i}+c^{*}\cdot sk_1 \end{aligned}$$

$\mathcal{A}$知道所有的$\bar{c_i},\bar{s_i}$和私钥$sk_1$，因此在$k-1$次调用后，$\mathcal{A}$完全能够计算$c^\ast ,s^\ast $。现在只要$c^\ast $满足

$$c^{*}=\sum_{i=1}^{k-1}\bar{c_i}=H(\prod_{i=1}^{k-1}R_i,m^{*})$$

即

$$H(\prod_{i=1}^{k-1}R_i,m^{*})=\sum_{i=1}^{k-1}H(\bar{R_i},m)$$

就可以通过验证。也就是说，如果能找到这样的$c^\ast $，那么$\mathcal{A}$能输出对$m^\ast \not =m$的伪造签名$\sigma^\ast =(c^\ast ,s^\ast )$.

构造k-sum问题

最后遗留下的问题是$\mathcal{A}$要找到合适$\bar{R_i}$，满足等式：

$$H(\prod_{i=1}^{k-1}R_i,m^{*})=\sum_{i=1}^{k-1}H(\bar{R_i},m)$$

这看起来是找哈希碰撞，生日攻击找到碰撞的时间复杂度是指数级别$O(2^{n/2})$，因此被看作是难以解决的。而在这里，要解决的问题是找到$k-1$个哈希值，使得它们的和等于另一个哈希值。这个问题被称作广义生日攻击，在02年Wagner提出一种k-tree的算法，可以在亚指数时间内进行广义生日攻击，后来也存在改进的算法。$k=2$时和生日攻击等价，这个问题表明，当$k$越大时，解决碰撞问题越容易.

广义生日攻击也叫k-sum问题。非正式地说，有$L_1,L_2,…,L_k$k个列表，每个列表中元素个数相同，列表中的元素都是$\mathbb{Z}_q$上均匀随机的元素，敌手要从每个列表中分别选择一个元素$x_1,x_2,…,x_k$，使得$x_1+x_2+\cdots+x_k \equiv 0(\bmod q)$。$q$的比特长度为$n$时，对每个列表，敌手能力搜索的范围$s_L=2^{n/(1+\lg k)}$，时间复杂度$\tau\in O(k\cdot 2^{n/(1+\lg k)})$。举个例子，当$k=4$时，每个列表搜索范围大小$s_L=2^{n/3}$，能够以不可忽略的概率在$O(2^{n/3})$找到符合条件的解.

要将我们之前的问题转化成k-sum问题，首先要构造$k$个列表，每个列表有$s_L$个元素。构造方法如下：

• $L_i,1\leq i < k$：随机选择$\bar{R_1},\bar{R_2},…,\bar{R_{s_L}}$，计算第$i$个列表的第$j$个元素$x_{ij}=H(\bar{R_j},m)$

• $L_k$：随机选择$m_1^\ast ,m_2^\ast ,…,m_{s_L}^\ast $，计算第$k$个列表的第$j$个元素$x_{kj}=q-H(\prod_{i=1}^{k-1}R_i,m_j^\ast )$

如果找到了k sum问题的解，那么用这$k-1$个$\bar{R_i}$在Challenge阶段作为挑战下发，Response阶段收到回复$\bar{s_i}$，$\mathcal{A}$就能按照以上方法构造出$\sigma^\ast =(c^\ast ,s^\ast )$.

$k$的选择影响k-sum求解的时间。对256比特的$q$，如果$\mathcal{A}$选择15条并发签名，在$2^{62}$步内可以完成攻击；如果$\mathcal{A}$选择127条并发签名，在$2^{45}$步内可以完成攻击。因此虽然这种攻击是亚指数，但仍然实用.

防御方法

构造k-sum问题过程中，发现列表需要足够多元素才可以完成攻击。一个想法是考虑缩小消息空间，让$m^\ast $的选择空间足够小，或者固定某个$m^\ast $，这样敌手就不能变换$m^\ast $来为$L_k$填充足够多的元素。但是这种方法并不可行，敌手可以选择一个随机数$a$来扩大空间：

$$\begin{aligned} c^{*}&=a\cdot \sum_{i=1}^{k-1}\bar{c_i} \\ s^{*}&=a\cdot \sum_{i=1}^{k-1}\bar{s_i}+c^{*}\cdot sk_1 \end{aligned}$$

容易验证这样$(c^\ast ,s^\ast )$也能通过签名验证，并且：

$$H\left(\left(\prod_{i=1}^{k-1}R_i\right)^a,m^{*}\right)\cdot a^{-1}=\sum_{i=1}^{k-1}H(\bar{R_i},m)$$

通过变换$a$来构造最后一个列表$L_k$.

亚指数攻击本质在于：敌手能够看到其它参与方的$R_i$之后再适应性地选择自己的$R_i^{\prime}$，这种攻击还能够拓展到门限签名。一种自然防御的方法是在$R_i$上再加一层承诺，比如今年美密上[Lin22]中的方案，但这种方法势必会增加轮数；还有一种方法是像这篇论文提到的mBCJ、FROST和后来的MuSig-2一样，在$R$和$m$之间建立起一种特殊的联系，只要$m$确定，那么潜在的全局$R$也会随之确定.

（思考：可证明安全都是多项式时间的敌手，怎样证明方案在亚指数下的安全性？）

参考文献

[1] M. Drijvers et al ., “On the Security of Two-Round Multi-Signatures,” 2019 IEEE Symposium on Security and Privacy (SP) , 2019, pp. 1084-1101, doi: 10.1109/SP.2019.00050.