“天融信杯”第四届全国高校数学挑战赛初赛及复赛。 今年及历年题目:竞赛官网地址
由于LaTeX数学公式较多,有时可能出现无法加载的情况,可以多刷新几次。
(2022.10注)
这篇文章是我2019年刚上大三时所写。当时学校的密码学课还没开,只打过一点CTF,偶然看到有这个比赛,和几个同学也就报了。19年CTF题目的难度也只是RSA的一些变体,几乎没有涉及ECC和Lattice的题目,而且这比赛知名度不像现在这么高,大家也不卷,答辩的时候评委们都很照顾我们,那时正逢暑假,也没有疫情,免费的烟台之旅特别轻松快乐。
所以直到现在,那都是对我来说很意义的一段时光,尽管这篇文章在我现在看来有很多理解不到位、甚至是错误的地方,但这很大程度上是我之后选择密码学研究的一个契机。
题目描述
题目文档里的描述很清晰,要我们解决的就是椭圆曲线上的离散对数问题(ECDLP)。ECDLP问题是椭圆曲线密码的核心技术问题,到目前为止,基于椭圆曲线有限域上的离散对数问题还没有真正有效的算法,是现代密码学中最具挑战性的问题之一。
ECC基本原理
设$\small \operatorname{F_{p}}$表示具有$\small p$个元素的有限域,其中$\small p>3$是一个素数。$\small {F_{p}}$上的椭圆曲线$\small {E}$是一个点集合$\small E/F_{p}= \{ ( x,y )\mid y^{2}= x^{2}+ax+b, a, b, x, y\in F_{p} \} \bigcup \{ \infty \}$,其中$\small {\infty}$表示无穷远点,$\small {4a^{2}+27b^{2}\neq 0(mod p)}$
设$\small {P= \small \left ( x_{1}, y_{1} \right )}$,$\small {Q=\small \left ( x_{2}, y_{2} \right )\in \small E/F_{p}}$,在$\small {E}$上定义$\small {“+”}$运算$\small {P+Q=R}$,$\small {R=\small \left ( x_{3}, y_{3} \right )\in \small E/F_{p}}$是过$\small {P, Q}$的直线与曲线另一交点关于x轴的对称点(当$\small {P=Q}$时,$\small {R}$是$\small {P}$点的切线与曲线的另一交点关于x的对称点).
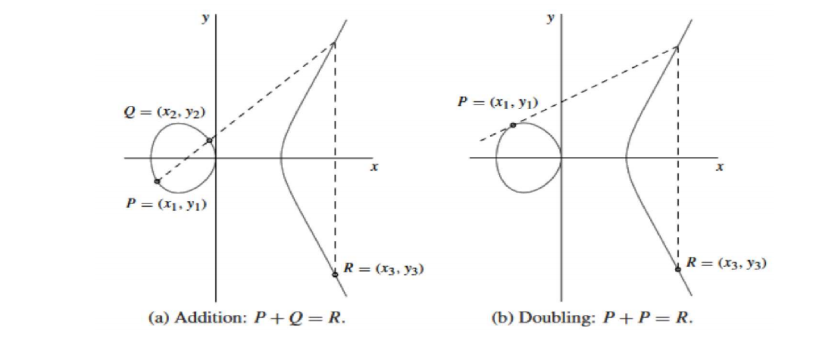
上述计算可用公式表示如下:
- 当$\small {P\neq Q}$时(Addition),$\small {R=\small \left ( x_{3}, y_{3} \right )=\left ( \left ( \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \right )^{2}-x_{1}-x_{2}, \left ( \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \right )\left ( x_{1}-x_{3} \right )-y_{1} \right )}$;
- 当$\small {P=Q}$时(Doubling),$\small {R=\small \left ( x_{3}, y_{3} \right )=\left ( \left ( \frac{3x_{1}^{2}+a}{2y_{1}} \right )^{2}-2x_{1}, \left ( \frac{3x_{1}^{2}+a}{2y_{1}} \right )\left ( x_{1}-x_{3} \right )-y_{1} \right )}$;
此外,对任意$\small {P=\small \left ( x_{1}, y_{1} \right )\in \small E/F_{p}}$,定义:
- $\small {P+\infty =\infty +P=P}$;
- $\small {\left ( x_{1}, y_{1} \right )+\left ( x_{1}, -y_{1} \right )=\small \infty }$,这里${\small \left ( x_{1}, -y_{1} \right )\in \small E/F_{p}}$。特别地,$\small {-\infty = \infty }$。
由此可验证$\small {E/F_{p}}$关于上述定义的$\small {“+”}$运算构成一个交换群,记为$\small {E\left ( F_{p} \right )}$。 设$\small {P \in E \left ( F_{p} \right )}$,记$\small {\left [ k \right ]P=P+P+\cdots +P}$(k times),则$\small {\left [ k \right ] \in \small E\left ( F_{p} \right )}$,该运算称为椭圆曲线标量乘法运算。设r为最小的正整数使得$\small {\left [ r \right ]\small P=\infty }$,r称为$\small {P}$的阶(order)。令$\small {\left \langle P \right \rangle=\left \{ \infty, P, \left [2\right]P, \cdots \left[r-1\right]P \right \}}$,可验证$\small {\left \langle P \right \rangle}$关于$\small {“+”}$运算构成$\small {E\left ( F_{p} \right )}$的一个r阶子群。 ECDLP:给定椭圆曲线$\small {E/F_{p}:y^{2}=x^{3}+ax+b}$,$\small {P\in E \left ( F_{p} \right )}$,r:=order$\small { \left ( P \right )}$,$\small {R \in \left \langle P \right \rangle}$,计算$\small {1\leq k\leq r}$,使得$\small {R=\left[k\right]P}$。(可形式化记为$\small {k=\log _{p}R }$)
ECDLP问题
其中n为椭圆曲线的阶#$\small {E \left ( F_{p}\right )}$,$\small {P}$是椭圆曲线上一点,r为P点的阶,即子群的阶;R位于子群中,且子群与群的阶满足拉格朗日定理,即有r|n。求运算次数k($\small {1\leq k\leq r}$)满足$\small {R=\left[k\right]P}$。
解题方法
特殊算法1:SSAS攻击异常椭圆曲线(有理点群阶等于有限域大小)上的ECDLP约化到有限域加法群的DLP,从而该类ECDLP存在多项式时间算法。 特殊算法2:MOV攻击利用椭圆曲线上的双线性对映射将定义在有限域$\small {F_{p}}$上的ECDLP归约到有限域乘法群$\small {F_{p^{k}}}$上的离散对数问题,此方法在嵌入次数k较小时有效。椭圆曲线子群阶r的嵌入次数k,即最小的正整数满足$\small {r\mid p^{k}-1}$。目前有许多研究证据表明,在一定假设情况下,有限域DLP存在亚指数时间算法。 通用算法:如Pollard’s rho算法、Pollard’s Kangaroo算法以及小步-大步法等均可用于求解一般有限群上的离散对数问题,其时间复杂度为$\small {O\left(\sqrt{r}\right)}$。
第一类ECDLP采用SSAS攻击 第二类ECDLP采用MOV攻击 第三类ECDLP采用通用算法Pollard’s rho 问题难度:第一类ECDLP<<第二类ECDLP<<第三类ECDLP 每类曲线按参数长度规模给出若干条实例,同类曲线相邻两小题计算复杂度相差约$\small {2^{8}=256}$倍。每类曲线的第一个实例问题,均可以在很短时间内完成,可以借助完成时间大致估计后续问题所需的时间、空间。
第一类曲线
第一类曲线参数:
(1) p:= 211108170305887; a:=0;b:=7;n:=p;r:=p;
P:=( 47815642535808, 116240163507508);
R:=( 77983503452527, 143728424564583);
(2) p:= 13835058061724614657; a:=0;b:=20;n:=p;r:=p;
P:=( 616859655854051956, 12065166484289278801);
R:=( 5170466145333976578, 7139090565738339416);
(3) p:=906694364778591846139117; a:=0; b:=2;n:=p;r:=p;
P:=(475325122433864976165476 ,666857317692667708141096 );
R:=(519814743429987512024682, 392414632044199857512746);
(4) p:= 59421121885714719481295537269; a:=0;b:=10;n:=p;r:=p;
P:=(17547290159953212409742744311, 23276625757393135830641872446);
R:=(22782721588122522786532109807, 29566916200346945584248955766);
(5) p:=3894222643901127098494944603540019; a:=0; b:=2;n:=p;r:=p;
P:=(3474281736844926688615305014567004, 3343311742974261537268420184037101);
R:=(46006664812763786791056435590121, 1631023347800240287678172773820495);
(6) p:= 255211775190703851000955237173238443091;
a:=0;b:=32;n:=p;r:=p;
P:=(82054120567654459070422632716611948091,
208358019881453692582450632924824868211);
R:=(54625405255845450735684923869953661538,
82751760415032967427013207973543496169);
(7) p:=16725558898897967356385545845388318567564081;
a:=0; b:=39;n:=p;r:=p;
P:=(15866255640827385375149316462253403735143979, 13637900016555731147592334085022810288787804);
R:=(1641844846280313158776293444944029290477363, 1916339757694211104728115095781816602417918);
(8) p:= 1096126227998177188652856107362412783873814431647;
a:=0;b:=5;n:=p;r:=p;
P:= (83173790821618364013911485269418053634749973470, 331912486564013055335956381322549180967694844964);
R:=(163008382252281273947629676562612579052560281605, 50645003441262331054159546612247657430098333396);题目分析:根据题目中所给的n,p可知该类椭圆曲线是$\small {F_{p}}$上的非正规椭圆曲线,即#$\small {E\left( F_{p}\right) =p}$。 核心计算:从$\small {E\left( F_{p}\right)}$到$\small {F_{p}}$加法群的同构映射。 原理:当椭圆曲线$\small {E\left( F_{p}\right)}$满足#$\small {E\left( F_{p}\right) =p}$,即Frobenius轨迹$\small {t=p+1-}$#$\small {E\left( F_{p}\right) =1}$,在线性时间内解决ECDLP问题。
- p-adic numbers 一个p-adic数能被表示为无穷级数形式,对应一个无穷级数数列:p-adic数构成的域为$\small {Q_{p}}$,特别地,当p没有负数幂时,构成的域记作$\small {Z_{p}}$。选择定义在p-adic数有限域上的椭圆曲线上的点,利用Lifts and Hensel’s Lemma提升引理映射到$\small {Q_{p}}$上。
- Lifts and Hensel’s Lemma 对于多项式$\small {f\left ( x \right )\in Z\left [ x \right ]}$,设x是f模$\small {p^{s}}$的根且u为$\small {f’\left( x\right) }$模p的模反元素。取x’:此时满足$\small {x’\equiv x\left ( mod\ p \right )}$,$\small {f\left ( x’ \right )\equiv 0\left ( mod\ p^{s+1} \right )}$.完成一次提升。 将$\small {E\left( F_{p}\right)}$中$\small {P,\ Q}$两点映射到$\small {E_{1}\left( Q_{p}\right)}$上两点$\small {P’,\ Q’}$,由$\small {E\left( F_{p}\right)}$上$\small {Q=kP}$可知$\small {Q’-kP’}$为$\small {E_{1}\left( Q_{p}\right)}$上的无穷远点,即模p下降转化为:
- p-adic椭圆对数 p-adic椭圆对数$\small {\varphi _{p}\left ( S \right )=-\frac{x\left ( S \right )}{y\left ( S \right )}}$提供了一个从$\small {E_{1}\left( Q_{p}\right)}$到$\small {pZ_{p}}$的同构。从而进行进一步转化:
攻击步骤:

实现代码(Sage script):
def SmartAttack(P,Q,p):
E = P.curve()
Eqp = EllipticCurve(Qp(p,2),[ZZ(t)+randint(0,p)*p for t in E.a_invariants() ])
P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
for P_Qp in P_Qps:
if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
break
Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
for Q_Qp in Q_Qps:
if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
break
p_times_P = p*P_Qp
p_times_Q = p*Q_Qp
x_P,y_P = p_times_P.xy()
x_Q,y_Q = p_times_Q.xy()
phi_P = -(x_P/y_P)
phi_Q = -(x_Q/y_Q)
k = phi_Q/phi_P
return ZZ(k)
p = 1096126227998177188652856107362412783873814431647
a = 0
b = 5
E = EllipticCurve(GF(p), [a, b])
P=E(83173790821618364013911485269418053634749973470,331912486564013055335956381322549180967694844964)
Q=E(163008382252281273947629676562612579052560281605,50645003441262331054159546612247657430098333396)
k = SmartAttack(P, Q, p)
print(k)
print(P*k == Q)第二类曲线
第二类曲线参数:
(9) p:= 140737488356467; a:=1;b:=0;
n:= 140737488356468; r:= 35184372089117;
P:=( 59477512413747, 79851403980273);
R:=( 125962305399026, 124644987166940);
(10) p:= 9223372036854782251; a:=1;b:=0;
n:= 9223372036854782252; r:= 2305843009213695563;
P:=(8930887567779448763 , 890632237231967440);
R:=( 4707122633993752935 , 3224323188778636920);
(11) p:=604462909807314587364667;a:=1;b:=0;
n:=604462909807314587364668; r:=151115727451828646841167;
P:=(587411173575122535454189, 184243119926212298785598);
R:=(539012794797204313781763, 513627008874848913042314);
(12) p:= 39614081257132168796771986051; a:=1;b:=0;
n:= 39614081257132168796771986052;
r:= 9903520314283042199192996513;
P:=( 17135037968192446511660916347 , 15756828316532436197954290560);
R:=( 14307140364976860571933505517 , 31289859728052046761658770776);
(13) p:=2596148429267413814265248164627363;a:=1;b:=0;
n:=2596148429267413814265248164627364;
r:=649037107316853453566312041156841;
P:=(622497953272208887929891881018762, 578415484635633376407094129167605);
R:=(1641315995010304174750922058961802, 498062680065145119027669812682594);
(14) p:= 170141183460469231731687303715884123283; a:=1;b:=0;
n:= 170141183460469231731687303715884123284;
r:= 42535295865117307932921825928971030821;
P:=(67561795560749592594257348250381095281 ,132967032564783335773794402620839168397);
R:=( 81767392472072972289932811718039895097 , 74483734086357842747707740743879456218);
(15) p:=11150372599265311570767859136324180753031283;a:=1;b:=0;
n:=11150372599265311570767859136324180753031284;
r:=2787593149816327892691964784081045188257821;
P:=(10280081406291279076050813261615407334758360, 10524832460733629896529554181939223304289725);
R:=(1653939556554266819965991031125172966638801, 8370614898071115688249737076845551200138218);
(16) p:= 730750818665451459101842416358141509827966272147; a:=1;b:=0;
n:= 730750818665451459101842416358141509827966272148;
r:= 182687704666362864775460604089535377456991568037;
P:=(221903508784709687556506235376523499020990986034 , 287854209568598432667871196372312232614552000893);
R:=( 219270464789952726868617287704232288912801490505, 578348937880270477205296252062048509994911317888);题目分析:
- 对于有限域$\small {F_{q}}$上的一条椭圆曲线$\small {E}$,其中$\small {q}$是$\small {p}$的幂,如果该曲线Frobenius轨迹t是p的倍数,则该曲线称为超奇异椭圆曲线,即$\small {p \mid q+1-}$#$\small {E\left ( F_{q} \right )}$。 特别地,当$\small {p}$为素数,$\small {p \equiv 3 \left ( mod \ 4 \right )}$且$\small {a \neq 0}$时,椭圆曲线$\small {E\left ( F_{p}\right ):y^{2}=x^{3}+ax}$是一条超奇异椭圆曲线。此时在$\small {F_{p}}$中对称分布$\small {p-1}$个点,再加上$\small {\left (0,\ 0 \right )}$和$\small {\infty}$两个附属点,可得#$\small {E\left ( F_{p}\right )=p+1}$,即$\small {t=0}$。
- 计算嵌入度:满足$\small {r\mid p^{k}-1}$的最小整数k值,作为扩域次数,同时也是椭圆曲线$\small {E\left ( F_{q} \right )}$上一对扭转点的嵌入度。扩域次数$\small {k \leq 6}$。 在第二类曲线题目中$\small {p,\ a}$均满足上述条件1,$\small {k=2}$满足条件2,可判断为MOV攻击。
核心计算:
- 从$\small {E\left ( F_{q} \right )}$的$\small {r}$阶子群到$\small {F_{p}^{k}}$乘法群的$\small {r}$阶单位根子群的同构映射(借助Tate配对或者Weil配对)。
- 计算$\small {F_{p}^{k}}$乘法群中的DLP。
原理: Weil对是一个函数$\small {e_{n}:E\left [ n \right ] \times E\left [ n \right ] \rightarrow F_{p}}$且具有下列性质:
- $\small {\forall S,\ S_{1},\ S_{2},\ T,\ T_{1},\ T_{2} \in E \left [ n\right ],\ }$ $\small {e_{n}\left ( S_{1}+S_{2},\ T \right )=e_{n}\left ( S_{1},\ T \right )e_{n}\left ( S_{2},\ T \right ), \ e_{n}\left ( S_{1}T_{1}+T_{2} \right )=e_{n}\left ( S,\ T_{1} \right )e_{n}\left ( S,\ T_{2} \right )}$
- $\small {e_{n}\left ( S,\ S \right )=1,\ \forall S \in E\left [ n \right ]}$
- $\small {e_{n}\left ( S,\ T \right )=e_{n}\left ( T,\ S \right )^{-1},\ \forall S,\ T \in E\left [ n \right ]}$
- $\small {e_{n}\left ( S,\ T \right )=1,\ \forall S \in E\left [ n \right ]\Leftrightarrow T=O}$ $\small {e_{n}\left ( S,\ T \right )=1,\ \forall T \in E\left [ n \right ]\Leftrightarrow S=O}$
mov归约的核心思想是利用一个Weil对将椭圆曲线上加法群中的离散对数问题映射到一个有限域乘法群的离散对数问题上。由于在乘法群中的离散对数问题方法是一致的,因此间接解决椭圆曲线上的离散对数问题。
攻击步骤:
 如果p为素数,$\small {q=p^{m}}$,在$\small {E\left ( F_{q} \right )}$的阶为$\small {q+1-t}$,可将超奇异椭圆曲线$\small {E}$分为六类:
如果p为素数,$\small {q=p^{m}}$,在$\small {E\left ( F_{q} \right )}$的阶为$\small {q+1-t}$,可将超奇异椭圆曲线$\small {E}$分为六类:
| Class | 条件 |
|---|---|
| I | ${\small t=0,\ E\left ( F_{q}\right ) \simeq Z_{q+1}}$ |
| II | ${\small t=0,\ q\equiv 3 \left( mod\ 4\right )}$且${\small E\left ( F_{q} \right ) \simeq Z_{\frac{q+1}{2}}\times Z_{2}}$ |
| III | ${\small t^{2}=q}$且${\small m}$为偶数 |
| IV | ${\small t^{2}=2q}$且${\small m}$为奇数 |
| V | ${\small t^{3}=3q}$且${\small m}$为奇数 |
| VI | ${\small t^{4}=4q}$且${\small m}$为偶数 |
选取${\small r_{1}}$时需要参照超奇异椭圆曲线的六种结构,对于超奇异椭圆曲线,点Q的选取更加简单。结构表如下:
| Class | ${t}$ | ${E\left ( F_{q}\right )}$ | ${r_{1}}$ | ${k}$ | ${E\left ( F_{q^{k}}\right )}$ |
|---|---|---|---|---|---|
| I | 0 | 循环 | ${\small q+1}$ | 2 | ${\small Z_{q+1}\times Z_{q+1}}$ |
| II | 0 | ${\small Z_{\frac{q+1}{2}}\times Z_{2}}$ | ${\small \frac{q+1}{2}}$ | 2 | $\small { Z_{q+1}\times Z_{q+1}}$ |
| III | ${\small \pm \sqrt{q}}$ | 循环 | ${\small q+1\mp \sqrt{q}}$ | 3 | ${\small Z_{\sqrt{q^3}\pm 1}\times Z_{\sqrt{q^3}\pm 1}}$ |
| IV | ${\small \pm \sqrt{2q}}$ | 循环 | ${\small q+1\mp \sqrt{2q}}$ | 4 | ${\small Z_{q^{2}+1}\times Z_{q^{2}+1}}$ |
| V | ${\small \pm \sqrt{3q}}$ | 循环 | ${\small q+1\mp \sqrt{3q}}$ | 6 | ${\small Z_{q^{3}+1}\times Z_{q^{3}+1}}$ |
| VI | ${\small \pm 2\sqrt{q}}$ | ${\small Z_{\sqrt{q} \mp 1}\times Z_{\sqrt{q} \mp 1}}$ | ${\small \sqrt{q} \mp 1}$ | 1 | ${\small E\left ( F_{q}\right )}$ |
选择II类${\small r_{1}=\frac{q+1}{2}}$(代码第13行)
实现代码(Sage script):
p = 9223372036854782251
r = 2305843009213695563
k = 2
F1 = GF(p, 'a')
F2 = GF(p^k, 'b')
phi=Hom(F1,F2)(F1.gen().minpoly().roots(F2)[0][0])
E1=EllipticCurve(F1,[1,0])
E2=EllipticCurve(F2,[1,0])
P1 = E1(8930887567779448763 , 890632237231967440)
R1 = E1(4707122633993752935 , 3224323188778636920)
P2 = E2(phi(P1.xy()[0]),phi(P1.xy()[1]))
R2 = E2(phi(R1.xy()[0]),phi(R1.xy()[1]))
Q = int((p+1) / 2r) * E2.random_point()
alpha = P2.weil_pairing(Q,r)
beta = R2.weil_pairing(Q,r)
print(beta.log(alpha))第三类曲线
第三类曲线参数:
(17) p:= 140737488355333; a:=-3;b:=234;
n:= 140737484527007;r:=n;
P:= (118344265104828, 25754556069705);
R:=( 8594518695631, 14966619423525);
(18) p:= 9223372036854775837; a:=-3;b:=37;
n:= 9223372038068412403;r:=n;
P:=(7220661838117791356 ,6477969291505257777);
R:=( 7819726923954549567 ,6266868167000835108);
(19) p:=604462909807314587353111;a:=-3;b:=95;
n:= 604462909807750541909849;r:=n;
P:=(428432040100075198254744, 95025782588400118295756);
R:=(472138605558837378507194, 138148835226095728614736);
(20) p:= 39614081257132168796771975177; a:=-3;b:=562;
n:= 39614081257132147751873462213;r:=n;
P:=(39220344157117715096559716859 , 3087260393566610895498596606);
R:=( 13160703755766149325136222951 , 6533567029273948676370251736);
(21) p:= 2596148429267413814265248164610099; a:=-3;b:=171;
n:= 2596148429267413788194246433592681;r:=n;
P:=(177627746966506201527866528484813 , 1735330667419561032038559795836927);
R:=( 1575178132453901115471501570466697, 538238983595050290992251454098891);
(22) p:= 170141183460469231731687303715884105757; a:=-3;b:=33;
n:= 170141183460469231728561996679834270597; r:=n;
P:=( 96152442714630401692673834213524521597 , 58626340067602219522071225434282008266);
R:=( 47795192678737921133501161460114957836 , 166078919686417913546029950371468891352);题目分析:经检验题目中所给的参数没有什么问题(实际上后来出题人说是按照ECC标准严格给的参数),因此考虑通用算法pollard’s rho。 核心计算:如何高效实现pollard’s rho及变体 原理: pollard’s rho算法的主要思想是寻找模n的不同$\small {\left ( c’,\ d’\right)}$和$\small {\left ( c’’,\ d’’\right)}$,使得
于是
且有
于是$\small k=\log_{p}R$可以通过计算
来得到。 定义一个迭代函数$\small {f:\left \langle P \right \rangle\rightarrow \left \langle P \right \rangle}$,使得给定$\small {X \in \left \langle P \right \rangle}$和$\small {c,\ d \in \left [ 0,\ n-1 \right ]}$且$\small {X=cP+dR}$,容易计算和$\small {\bar{c},\ \bar{d} \in \left [ 0,\ n-1 \right ]}$且$\small {\bar{X}=\bar{c}P+\bar{d}Q}$。此外,函数$\small {f}$还要具有随机性。 现在任一点$\small {X_{0}\in \left \langle P \right \rangle }$确定一个点序列$\small \left \{ X_{i} \right \}_{i \geq 0}$,其中对于$\small {i\geq 0}$有$\small {X_{i}=f\left (X_{i-1} \right )}$。因为集合$\small {\left \langle P \right \rangle}$是有穷的,序列终将产生碰撞并进入循环;也就是说,对于$\small {s \geq 1}$,存在最小的序列$\small {t}$使得任意的$\small {X_{i}=X_{t+s}}$,且对所有的$\small {i \geq t+s}$有$\small {X_{i}=X_{i-s}}$。这里$\small {t}$称为序列的尾长度,$\small {s}$称为序列的循环长度。若假设$\small {f}$为随机函数,则序列出现首次碰撞的预计步数为$\small {\sqrt{\frac{\pi n}{2}}}$。此外,预计的尾长度为$\small {t\approx \sqrt{\frac{\pi n}{8}}}$,循环长度为$\small {s\approx \sqrt{\frac{\pi n}{8}}}$。 一个碰撞,即对点$\small {X_{i},\ X_{j}}$有$\small {X_{i}=X_{j}}$且$\small {i\neq j}$,可以用Floyd循环查找算法来计算。该算法对于$\small {i=1,\ 2,\ 3\cdots }$计算点对$\small {\left ( X_{i},\ X_{2i}\right )}$直到$\small {X_{i}=X_{2i}}$。计算出新的点对以后可以将老的点对丢弃,因此其需要的存储空间近于零。预计得到$\small {\left ( X_{i},\ X_{2i}\right )}$之前计算这些点对的次数$\small {k}$显然满足$\small {t\leq k\leq t+s}$。事实上,假定$\small {f}$是随机函数,则预计值$\small {k}$约为$\small {1.0308\sqrt{n}}$,因此预计的椭圆曲线群运算次数约为$\small {3\sqrt{n}}$。算法失败的概率趋近于0。 出题老师在讲解这道题时提到涉及的三个技巧:(1)高效有限域算术 (2)高效椭圆曲线算术(利用$\small {a=3}$以及射影jacobi坐标) (3)并行化技术 高效的有限域算术和椭圆曲线算术,同样可以提高Pollard’s rho算法实现效率,利用state-of-the-art的有限域/椭圆曲线算术,可比Magma/Sage等相应实现效率高很多。
实现代码(Sage script)
p = 9223372036854775837
a = -3
b = 37
r = 9223372038068412403
E = EllipticCurve(GF(p), [a, b])
P = E(7220661838117791356, 6477969291505257777)
Q = E(7819726923954549567, 6266868167000835108)
print(discrete_log_rho(Q, P, ord=P.order(), operation='+'))计算实现环境及结果
实现环境 CPU型号:Core i5-7300HQ 内存:16G ddr4 运行结果 每类曲线参数位数越多,分值越高。总分由每类曲线最高分相加。分数相同的队伍依照难度最高的挑战求解时间来排序,求解用时越少者排名越靠前。计算结果如下:
 第一类曲线运行时间比较正常,秒出答案;第二类曲线运行时间相对较短(如果资源好能再出新答案);第三类曲线由于没有高效实现Pollard’s rho算法,运行时间较长。
第一类曲线运行时间比较正常,秒出答案;第二类曲线运行时间相对较短(如果资源好能再出新答案);第三类曲线由于没有高效实现Pollard’s rho算法,运行时间较长。
ECC的安全性
公钥密码体制根据其所依据的难题一般分为三类:大素数分解问题、离散对数问题、椭圆曲线上的离散对数问题。 椭圆加密算法(ECC)是一种公钥加密体制,由Koblitz和Miller两人提出,其数学基础是利用椭圆曲线上的有理点构成阿贝尔加法群上椭圆离散对数的计算困难性。 相对于RSA加密算法,ECC的主要优势是可以在某些情况下使用更小的密钥,但仍提供相当的或更高等级的安全,有研究表示160位的椭圆密钥与1024位的RSA密钥安全性相同ECC算法的单位安全强度高于RSA算法。ECC的另一个优势是可以定义群之间的双线性映射,基于Weil对或是Tate对,可以用于基于身份的加密。对于ECC系统,目前公认最有效的方法式Pollard’s rho算法,但它求解的破译或求解难度基本上是指数级的,只要避免使用特殊曲线,破解ECC依然很困难。 ECC选择参数标准:
- 为了抗击Pollard-ρ攻击,所选取椭圆曲线的阶#$\small {E\left( F \left (p\right )\right )}$的分解式中英包含一个大的素因子,目前应不小于160bit;
- 为了抗击Weil对和Tate对的攻击,对于$\small {1\leq k\leq 30}$,$\small {n}$不能整除$\small {p^{k}-1}$(不宜选取超奇异椭圆曲线);
- 为了抗击SSAS攻击所选曲线的阶不能等于该曲线所定义的有限域的阶,即#$\small {E\left( F_{p}\right) }$(不宜选取异常椭圆曲线);
- 对于二进制域$\small {F\left( 2^{m}\right )}$的度不宜为合数。若$\small {m}$有小约数$\small {l\left ( l=4\right )}$,存在比Pollard’s rho算法更快求解ECDLP的方法。
- 选择$\small {E\left( F_{p}\right )}$的子域$\small {H}$,满足它的阶$\small {|H|}$是#$\small {E\left( F_{p}\right )}$的最大素因子$\small {n}$,并在$\small {H}$上实现ECC。
参考文献
1 Richard E.Blahut.Cryptography and Secure Communication[M].Cambridge University Press and China Machine Press:China,2018:270. [2] Darrel Hankerson,Alfred Menezes,Scott Vanstone.Guide to Elliptic Curve Cryptography[M].Spring:New York,2003:153. [3] Peter Novotney.Weak Curves In Elliptic Curve Cryptography[J].novotney,2010,5:1-9.
推荐参考文献 第一类曲线 [4] Smart N P,The Discrete Logarithm Problem on Elliptic Curves of Trace One[J].Journal of Cryptology,1999,12(3):193-196 [5] 祝跃飞,裴定一.求异常曲线上的DLP的一个算法[J].中国解学:2001.31(4):332-336 第二类曲线 [6] Frey.G.Ruck,H:A Remark Concerning m-divisibility and The Discrete Logarithm in The Divisor Class Group of Curves.Math.Comp,62.865-874(1994) [7] Menezes A.J.Okamoto T.Vanstone,S.A:Reducing elliptic curve logarithms to logarithms in a finite field, IEEE trans,Inf Theory,39(5),1639-1646(1993) 第三类曲线 [8] Pollard J.M,AMonte Cario method for index computation (modp).Math,Comput,32(143),918-924(1978) [9] Bailey D.Batina L.Bernstein D.J.Birkner P,Bos J.W,et al:Breaking ECC2K-130.Cryptology ePrint Archive,Report 2009/541(2009)
- 本文链接: https://qsang.xin/2019/08/19/cmsecc2019/
- 版权声明: 本网站所有文章除特别声明外,均采用 CC BY-NC-ND 4.0 许可协议。转载请注明出处!